How I learned to stop worrying and love the capital gains tax

[Al B. Sure!]

I know cross-posting isn't allowed but this in the other thread was getting a bit fuddled with other things and I want to attract some of our more economics savvy posters on this topic. I kind of feel like I'm doing something wrong but it's making sense to me logically.

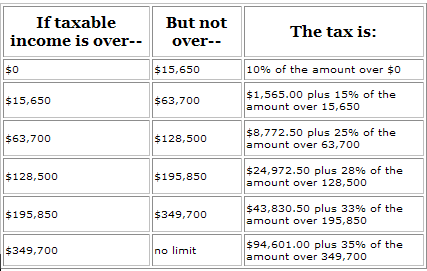
Now, Kuciwalker was trying to make the point that a Capital Gains tax is unfair because it increases the effective tax rate for investors. I agree with this but same that taketh can giveth, it seems. Check it:

I have a scenario. Same as kuci's with Bob and Alice but slightly different...

Tax regime A is a flat 20% income tax - including interest and capital gains as income. Tax regime B is a flat 20% earned income tax, i.e. it excludes interest and capital gains.

Alice and Bob each earn $1000 at the end of 2010. They can spend some portion of the money now on stuff they want now, or they can invest that money in a security. Alice chooses to spend all $1000 right now, and Bob chooses to spend $500 now and invest $500 in a security. Now, unbeknownst to him, his investment is a dud and drops 50% in value and he sells it at a loss. So poor Bob, in a non-taxed environment, has only $750 to spend (500+(500*.50)).

Under tax regime A, Alice only actually gets to spend $800 now, so she has an effective tax rate of 20%. Under tax regime B, she still only gets to spend $800 now, so she still has an effective tax rate of 20%.

Under tax regime A, Bob gets to spend $400 now. He gets to invest $400. Now, Bob is unlucky and he sells the security at a loss. The security cost him $400 and he sold for $200 (the same 50% loss in value) for a loss of $200. In total he gets to send $400 + $200 = 600. But, fortunately, his capital losses reduce his income tax liability...

Now, the government demands 20% of all income. Before, when Bob earned $1000, he was taxed at this 20% rate for $200, leaving him with $800 to do as he pleased with. He has a $200 tax liability.

When it comes for tax time, however, his income for the year was only $800 once he deducted capital losses ($1000-$200 in capital losses). $800 at 20% tax rate leads to a tax liability of $160 (alternatively, $200 in losses*20% to get his overpayment). He overpaid $40 in taxes and will get that back. So now, he has $640 to spend.

Now what is his effective tax rate? 100*($750-$640)/$750= 14.67%, which is lower than 20% - Bob is paying a smaller proportion of his income than Alice, he's benefiting from taking a risk and investing rather than spending all his money at once.

Now before you cry foul and say, well wait, he lost $250 in the non-taxed environment and only $200 in the taxed because he had $100 less to invest. That brings us to 100*($800-$640)/$800= 20%. This reflects directly the $160 in actual taxes paid only.

Now, under tax regime B, Bob gets to spend $400 now. He gets to invest $400 and loses $200 but he can not deduct capital losses. In total he gets to spend $400 + $200 = $600. 100*($750 - $600)/$750 = an effective tax rate of exactly 20%. Or, alternatively, to reflect actual taxes paid only, 100*($800-$600)/$800= an effective rate of 25%. Under tax regime B, Bob IS penalized for investing his money rather than spending it all at once.


The same that giveth can taketh away it seems. Take it from someone who lost $9K speculating on Citigroup and AIG options in the winter of 2008/2009, being able to deduct capital losses is peachy keen by me.

This other side of the coin, this benefit of the capital gains tax law with regards to losses, should be considered when tallying the effective tax rate with regards to capital gains. Now, of course, it is limited by $3000/tax year so there's that. I'm sure you could come up with a nifty little equation where you could put in different probabilities of different gains/losses, constrained on the downside by the $3000 cap on capital losses, and the resulting effective tax rates under conditions of uncertainty.

[Al B. Sure!]

Now here's an aside I noted just fooling around with things at 5 am:

Well it's late and I haven't messed around with numbers like this in three years so forgive any mistakes but I came up with...

effective tax rate= 100*[(I*PsubscriptN*(1+N))-(((I*(1-T))*(1+(PsubscriptN*N)*(1-T)))]/(I*PsubscriptN*(1+N))

where N is the % increase/decrease in value of a security, PsubscriptN is the probability of N for all N, and T is the nominal tax rate.

The basic intuitive thing is that losses up to $3000 offset equivalent gains for tax purposes because of the benefit in tax deduction but I'm not sure exactly how to represent it in the equation (can't think right now how to do it so it's not represented in the equation except as a constraint relating to N I suppose). Beyond that though, obviously, the disadvantages of tax become apparent and the ETR approaches or exceeds the nominal TR.

Fooling around with it, assuming a 20% tax rate (including on capital gains), with a $3000 capital loss maximum deduction, and a $10,000 initial investment (well, it's taxed at 20% so $8000 investment), the security can dip to a loss of 38% (8000*(1-.38)=~5000) before hitting the $3000 capital loss wall. That leaves an ETR of 10.4% or a mere 52% of the nominal TR. If the value increases by 38%, the ETR is 24.4% (122% of the NTR). So at these points, I can pay 52% of my initial tax if I lose $3000 or 122% of my initial tax if I make $3000.

At higher tax rates, this disparity in the % of the nominal that the ETR is between a 38% loss and a 38% gain closes (at 50% nominal TR, the ETR as % of NTR becomes 70% and 113% respectively). So higher nominal TR results in weakened tax benefits from capital losses but also ETR's closer to the nominal TR on the positive gain side. Makes sense, as you approach 100% NTR, ETR should approach 100%. Kind of funny. At higher tax rates, ETR approaches NTR. Higher tax rates!

Now, at higher gains, all else being equal, ETR as a % of NTR increases but at a decreasing rate (1%->2% gain, ETR as % of NTR increases by 0.77 or 0.7% increase, 40%->41% ETR as % of NTR increases by 0.40 or 0.3%). These changes in the ETR as % of NTR get smaller overall and more narrow between different gain levels as the tax rate increases (At 40% tax rate, 1%->2% gain, 0.58 or 0.57%; 40%->41%, .30 or 0.25%).

I know I'm rambling sorry it's late. The point is, I think, could be wrong, tired, but if you put in the probabilities of different investment outcomes then you have a handy little tool for determining the most tax efficient allocation of investments in a portfolio at different tax rates (too bad you can't really control this variable legally). haha not really relevant to this thread i guess. God it's been a long time since I did anything financial. I feel like I'm overlooking something d'uh.

a response to Kuci:

Kuci:

http://www.irs.gov/newsroom/article/0,,id=106799,00.html

# If your capital losses exceed your capital gains, the excess can be deducted on your tax return and used to reduce other income, such as wages, up to an annual limit of $3,000, or $1,500 if you are married filing separately.

I should know. Like I said, I took full value of the capital loss deduction for 2009 and will be using it the next two years.

Now...

From Kuci: Even if it did work, all you would have shown is that a capital gains tax provides favorable rates to people who make bad investments. ...why is this a good thing?

Umm... it means that the unfavorable tax situation on the plus side is compensated by the favorable tax situation in case of loss (ie- all investments involving capital gains are made under conditions of uncertainty so you have to take your lumps with your gains) so what I'm saying is up until a loss of $3000, the plusses and minuses of a CG tax with regards to ETR balance out under conditions of uncertainty. This is a very important point.

From Kuci: edit: your 25% figure is not sensibly calculated. The $800 is pre-investment but the $600 is post-investment.

Look, what you yourself was calculating was the effective tax rate. The effective tax rate by definition is the actual tax paid divided by net taxable income, expressed as a percentage. That is why using $750 is not quite accurate because he wouldn't be taxed on that (the issue is the difference in losses... he losses less money in absolute terms with a tax because he had less money to invest). He would instead be taxed on $800, which is the $1000 original minus his $200 in capital losses.

So there you go.

Could anyone else a bit more seasoned in financial modeling help out a bit. Did I make some errors? Or could you explain it in a way that a CS grad like Kuci could understand?

[Al B. Sure!]

And the latest:

From Kuci: Only if you are just as likely to be losing money on your investments as gaining. Do you really want to penalize saving by intelligent investors but reward it by really dumb ones?

Umm... What are you not understanding? Under conditions of uncertainty (WHICH ARE ALL INVESTMENTS WHICH CAN POSSIBLY CAUSE CAPITAL GAINS!)! It's not about dumb investors. It's about the fact that...

Here let me make it real simple even a CS grad can understand:

You stated the tax disadvantages of a capital gains tax on positive capital gains (ie- higher effective tax rate than if the capital gains were un-taxed). That is completely true. What I am pointing out is that there are tax ADVANTAGES of a capital gains tax on negative capital gains ie- losses (ie- lower effective tax rate than if the capital gains were un-taxed).

Now, what that means is that on any particular investment (well EVERY investment that allows for the possibility of capital gains [capital gains tax does not equal tax on interest or dividends), the outcome is uncertain. It's not about smart or dumb investors. The only difference between a smart and a dumb investor is a smart investor does more research and minimizes his risk exposure but that doesn't mean he operates under any more certainty on the success of any particular security than the dumb investor (learn some basic portfolio theory).

So the point is, the advantages and disadvantages nullify each other under conditions of uncertainty (which all investments that allow for capital gains are under). There is a cap on this though at $3000 loss per tax year. So the tax advantages of losses beyond that do not nullify the tax disadvantages of corresponding percentage gains.

The net result is the capital gains tax increases one's effective tax rate under conditions of uncertainty but only in conditions when the gains or losses exceed the loss value that would result in a $3000 loss (ie- for $10K income, $8K invested due to 20% tax rate, 38% loss or gain is this point; The capital gains tax has no effect on tax rate between a loss of 38% and a gain of 38%).

From Kuci: No, the effective tax rate by definition is the proportion of money you no longer have compared to the no-tax scenario.

Read a book. Really, you are not knowledgeable enough to speak on any of this stuff.

http://www.investorwords.com/1668/effective_tax_rate.html

"Actual income tax paid divided by net taxable income before taxes, expressed as a percentage."

http://www.ncnblog.com/2007/11/16/a-bit-about-taxes-understanding-effective-tax-rates-for-2007-planning-for-2008/

there's a little about calculating ETR for IRS purposes.

By definition my ass... Where did you pull that from? Are you just making things up now?

From Kuci: Your definition makes meaningful comparison between tax schemes impossible.

Um... no, it still works. ETR as properly defined is still valid but because I admit having less money to invest kind of saved someone from losing money, I included both calculations in my analysis of the two schemes. Either way, the point remains that when one losses money, he's better off having a capital gains tax than none.

And to re-iterate once again, this means that the advantages/disadvantages under losses/gains nullify each other up until a $3000 cap because investments are made under conditions of uncertainty.

(and technically, because that $3000 cap is only for a specific tax year and can be carried over into other years (ie- $10K in losses can be carried 3000 in years 1, 2, and 3, and $1000 in year 4)... well, it's a bit more complicated but you can progressively increase the possible gains/losses on an asset beyond let's say 38% in my previous scenario, constrained only by the Present Value of the future tax rebates).